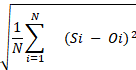Boletín geográfico. Año XLVI. N°46 - 2024, pp. 1-16 Departamento Geografía. Universidad Nacional
Boletín geográfico. Año XLVI. N°46 - 2024, pp. 1-16 Departamento Geografía. Universidad Nacional
del
Comahue. Neuquén
ISSN 0326-1735 ;
e-ISSN 2313-903X
ark: http://id.caicyt.gov.ar/ark:/s2313903x/ykja7shwa
http://revele.uncoma.edu.ar/htdoc/revele/index.php/geografia/index
VALIDACIÓN DE PRECIPITACIÓN ESTIMADA POR CHIRPS
EN UNA REGIÓN SEMIÁRIDA DE
ARGENTINA
Yamila Lambrecht1 Anabella Montico1 Natasha Picone1,2
(Manuscrito recibido el 21 de diciembre de 2023, en versión
final 21 de mayo de 2024)
Para citar este documento
Lambrecht, Y., Montico, A. & Picone,
N. (2024). Validación de precipitación estimada
por CHIRPS en una región semiárida de Argentina. Boletín
geográfico, 46, http://id.caicyt.gov.ar/ark:/s2313903x/ykja7shwa.
Resumen
Los
datos grillados de precipitación son una herramienta valiosa en contextos de
escasez de datos observacionales. Para su uso es fundamental la validación a
través de análisis estadísticos. El objetivo del trabajo es validar la base de
datos CHIRPS (Climate Hazards
Group InfraRed Precipitation with Station Data, por sus siglas en inglés) para el suroeste de
la provincia de Buenos Aires a lo largo del período 1990- 2020. Este conjunto
de datos posee una adecuada cobertura espacio-temporal
para estudiar la variabilidad de las precipitaciones dado que presenta
cobertura diaria y continua desde 1980 hasta
la actualidad con una resolución de
0,05° entre los 50°S y 50°N. Para
la validación, se aplicaron el coeficiente de correlación de Pearson (r-
Pearson), el error absoluto medio (mae), el error cuadrático medio (rmse) y el sesgo porcentual (pbias),
en entorno R utilizando el paquete hydroGOF. CHIRPS
presentó correlaciones de entre 0,68 y 0,84 respecto a los datos observados,
tanto a escala mensual como anual. Asimismo, se observó una tendencia a
sobreestimar las precipitaciones entre 2 y 4% a escala mensual, excepto en el sector noroeste,
donde
1Consejo Nacional de Investigaciones Científicas y Técnicas
(CONICET). Departamento de Geografía y Turismo,
Universidad Nacional del Sur (UNS), 12 de octubre 1098, 4º piso, Bahía Blanca,
Buenos Aires, Argentina. E-mail: yamila.lambrecht@uns.edu.ar anabella.montico@uns.edu.ar
2 Centro de Investigaciones Geográficas, Instituto de Geografía, Historia y Ciencias Sociales,
Facultad de
Ciencias Humanas,
Universidad Nacional del Centro de la Provincia de Buenos Aires,
Consejo Nacional de Investigaciones Científicas y Técnicas
(CIG/IGEHCS, FCH, UNCPBA/CONICET).
1
se
subestimaron entre 4 y 11%. A escala anual la sobreestimación se situó entre 3
y 4% mientras que la subestimación presentó las mismas características que a
escala mensual. El análisis de mae y rmse evidenció
mayores errores en las estaciones próximas al cordón serrano en ambas escalas
temporales. Se concluye que CHIRPS es aplicable para estudios de variabilidad de las precipitaciones en la región
analizada, principalmente a escala anual, donde la falta de datos se
presenta como un problema recurrente, teniendo en cuenta los errores espaciales
detectados y las menores diferencias en las correlaciones entre estaciones de
anclaje y fuentes independientes para estudios climáticos a esta escala.
Palabras clave: CHIRPS,
datos grillados, validación,
precipitaciones, suroeste de la provincia de Buenos Aires.
VALIDATION OF CHIRPS
ESTIMATED PRECIPITATION IN A SEMI- ARID REGION OF ARGENTINA
Abstract
Gridded data of precipitation are a valuable
tool in scarce-observational data contexts. Validation through statistical analysis is essential for its use. This work aims
to validate the Climate Hazards Infrared Precipitation with Stations (CHIRPS)
database for the southwest of Buenos Aires province over the period
1990-2020. This dataset has
adequate spatio-temporal coverage to study rainfall
variability since it presents daily and continuous coverage from 1980 to the present with
a resolution of 0.05° between 50°S
and 50°N. For validation purposes, Pearson's correlation coefficient
(r-Pearson), mean absolute error (mae), root mean
squared error (rmse) and percent bias (pbias) were applied in the R environment using the hydroGOF package. CHIRPS shows a correlation between 0.68
and 0.84 for observed data on both monthly and annual scales. It also tends to overestimate rainfall
between 2 and
4%on a monthly scale,
except in the northwestern sector,
where it was underestimated
between 4 and 11%. At the annual scale, overestimation was between 3 and 4%, while
underestimation presented the same characteristics as at the monthly scale. The
analysis of mae
and rmse showed
greater errors in the stations
near the mountain
range at both time scales. It is
concluded that CHIRPS is applicable
for rainfall variability studies in the analyzed region, where the lack of data
is a recurrent problem, considering the spatial errors detected.
Keywords: CHIRPS,
gridded data, validation, precipitation, southwest of Buenos Aires province.
Introducción
La precipitación es una variable
atmosférica de gran relevancia en la gestión de los
recursos hídricos tanto por la disponibilidad de agua como así también por los
peligros asociados a eventos de larga duración y/o intensidad. El estudio de la
precipitación puede abordarse desde diferentes aristas, entre ellos los
forzantes que influyen en la variabilidad espacio-temporal, los cambios y
tendencias y el potencial erosivo Por ejemplo existen trabajos acerca de las
anomalías de temperatura de la superficie del mar (TSM) en el Pacífico
Ecuatorial e Índico Occidental (asociadas a la teleconexión
El Niño-Oscilación del Sur (ENSO)) que inducen anomalías en la circulación y
así favorecen el desarrollo de precipitaciones intensas en el sureste de
Sudamérica (SESA) (Robledo,
Penalba & Bettolli, 2013; Olmo, 2023)..
Por otra parte, los índices de precipitación
permiten estudiar fenómenos climáticos extremos y monitorear el cambio
climático. Particularmente, se han documentado numerosos trabajos donde se
aplican índices elaborados por el Equipo de Expertos en Detección
e Índices del Cambio Climático (ETCCDI) de la Organización Meteorológica
Mundial (OMM) (Serrano-Notivoli, Beguería,
Saz & De Luis, 2018; Bezerra, Silva, Santos e Silva & de Carvalho, 2019). Una metodología implementada a menudo
para representar la relación
entre la intensidad, duración y frecuencia (o período de retorno)
son las curvas IDF, para las cuales se utilizan con frecuencia productos
basados en estimaciones satelitales (Ombadi, Nguyen, Sorooshian & Hsu, 2018; Mianabadi, 2023). En muchos casos, la precipitación se
estudia con el objetivo de abordar el problema de la erosión hídrica. Para ello se
aplican diversos índices, entre los
que se destacan el índice
de Fourier (Fourier, 1960), el índice
de concentración (Martín-Vide,
2004) y el factor R (Wischmeier, 1959), entre otros.
La ocurrencia de precipitaciones intensas ocasiona con frecuencia impactos
negativos
en áreas urbanas y rurales. La escasa disponibilidad de datos de calidad limita la comprensión de la ocurrencia de eventos extremos
y sus impactos asociados (Salih
et al., 2023). Entre los impactos de
las precipitaciones se destacan los anegamientos e inundaciones por colapsos en
el sistema de drenaje urbano y desbordamiento
de ríos, erosión
hídrica, deslizamiento de laderas, entre
otros (Ávila- Parra &
Martín-Vide, 2013). En las regiones semiáridas, las
precipitaciones intensas ocurren con frecuencia
y generalmente las mismas no cuentan
con herramientas para enfrentarlas (Marianetti & Rivera, 2021). Por ello, conocer su
comportamiento es necesario para proponer e implementar políticas de gestión y acciones de adaptación que minimicen los impactos
adversos que éstas ocasionan (Lovino, 2015).
Una de las cuestiones que emergen con frecuencia en el
estudio de la precipitación es la disponibilidad de datos actualizados y confiables. La incertidumbre
observacional producto de la escasez
de datos es notoria en gran parte de Sudamérica
debido al elevado costo de mantener una red densa activa de estaciones
meteorológicas (Olmo, 2023). La obtención de datos confiables de precipitación
es vital para la planificación y gestión de los recursos hídricos (de Moraes Cordeiro & Blanco,
2021). Frente a este contexto, las estimaciones a través de satélites
constituyen una valiosa herramienta complementaria a las observaciones para
aplicaciones hidrológicas y climáticas vinculadas a la gestión
del recurso hídrico,
dada su alta resolución temporal y cobertura
cuasi-global
(Hobouchian,
Salio, Skabar, Vila
& Garreaud, 2017; Saucedo,
Kurtz & Contreras, 2023). Argentina posee una baja cantidad de estaciones
meteorológicas y su distribución espacial es heterogénea ya que la mayoría se
concentra en el centro del país, dejando a las regiones del norte y sur con muy
poca cobertura de observaciones (Lúgaro, 2022). En el área de estudio,
emplazada en el suroeste bonaerense, la situación es similar dado que cuenta
con sólo cuatro estaciones del
Servicio Meteorológico Nacional (Bahía Blanca Aero, Pigüé Aero, Coronel Suárez
Aero y Coronel Pringles Aero) y con dos estaciones del Instituto
Nacional de Tecnología Agropecuaria (INTA) (Hilario Ascasubi y Bordenave). En
este contexto, Casado y Picone (2018) evaluaron el potencial de las series
grilladas del Global Precipitation Climatology Centre (GPCC) para la provincia de Buenos Aires
a escala mensual y anual (1911-2000). Como resultado, obtuvieron una
variabilidad de ajuste entre 60 y 99%. Del análisis de la variabilidad de la
precipitación a escala anual, decádica y climática las autoras concluyen
que la base de
datos describe
correctamente las tendencias de distribución espacial
y de variabilidad temporal.
La base de datos CHIRPS (Climate
Hazards GroupInfra Red Precipitation with Station Data, por sus siglas en inglés) fue desarrollada
por el Servicio Geológico de los Estados Unidos (USGS) en colaboración con el
Grupo de Riesgos Climáticos de la Universidad de California en Santa Bárbara.
Posee datos de precipitación provenientes de observaciones y estimaciones
satelitales, con una cobertura casi global desde el año
1981 hasta el presente con una resolución de 0,05° entre
los 50°S y 50°N (Funk et al., 2015). Sin embargo, para su
aplicación práctica es necesario validar su rendimiento (Arregocés, Rojano & Pérez, 2023).
Existen diversos estudios sobre validación de estimaciones
de este tipo y, particularmente, del producto CHIRPS. Este aspecto ha sido
estudiado por distintos autores a nivel mundial (Alsilibe, Bene, Bilal, Alghafli & Shi, 2023; Bai, Shi, Li, Shang &
Wu, 2018; Prakash, 2019).
Particularmente, en Latinoamérica se destacan los trabajos realizados en
Colombia (Arregocés et al.,
2023), Brasil (Cavalcante et al.,
2020), Chile (Zambrano, Wardlow, Tadesse, Lillo-Saavedra & Lagos, 2017) y la zona cordillerana de los Andes subtropicales de Argentina y Chile (Hobouchian et al.,
2017), entre otros. En Argentina, existen antecedentes en el uso de CHIRPS.
Medina, Zossi, Bossolasco y
Elias (2023) analizaron el desempeño de CHIRPS
comparando las regiones NEA y NOA. Particularmente en Corrientes, Saucedo et al. (2023) validaron CHIRPS junto con
las bases Tropical Rainfall Measuring
Mission (TRMM) y Global Precipitation
Measurement (GPM) a escala anual (2000-2019). En
Córdoba, Gusmerotti, Posse,
Oricchio, Rivadeneira y Di Bella (2023) evaluaron el comportamiento de CHIRPS y propusieron una técnica de corrección a través de datos de estaciones meteorológicas. En los Andes Centrales,
Rivera, Marianetti y Hinrichs
(2018) concluyeron que CHIRPS reproduce adecuadamente la variabilidad
estacional e interanual de la precipitación en el período 1987-2016 hasta los
1000 m.s.n.m., donde el desempeño se reduce notablemente. En el contexto de
falta de datos y dada la disponibilidad y potencialidad de CHIRPS, el objetivo de este trabajo
es validar esta base de datos para un área del suroeste de la provincia de Buenos Aires, Argentina,
en el período 1990- 2020.
Área de estudio
El área de estudio constituye el límite meridional de la
llanura pampeana argentina (Campo,
Diez & Capelli de Steffens, 2004)
y está formada por los partidos de Coronel
Suárez, Saavedra, Puan, Tornquist, Coronel Pringles, Bahía Blanca y Villarino
(Figura 1). Estos se seleccionaron debido a la escasa cobertura de la red de estaciones meteorológicas y la potencialidad de CHIRPS para complementar los datos
derivados de estas. Se encuentra dentro de los climas templados y se
caracteriza por una variabilidad espacial
y temporal de las precipitaciones, dando lugar a ciclos secos y húmedos (Campo et al., 2004; Gil, Gentili, Campo, Jelinski, & Crisafulli, 2016;
Aliaga, Ferrelli & Piccolo, 2017).
En este sentido, el sistema
de Ventania produce
un efecto orográfico que incide en el comportamiento y los montos de
precipitación (Gentili & Gil, 2013; Gil et
al., 2016; Volonté, 2017). Asimismo, el régimen de precipitación presenta
una marcada estacionalidad con una estación lluviosa de octubre a marzo y una
estación relativamente seca de mayo a septiembre (Casado & Campo, 2019).
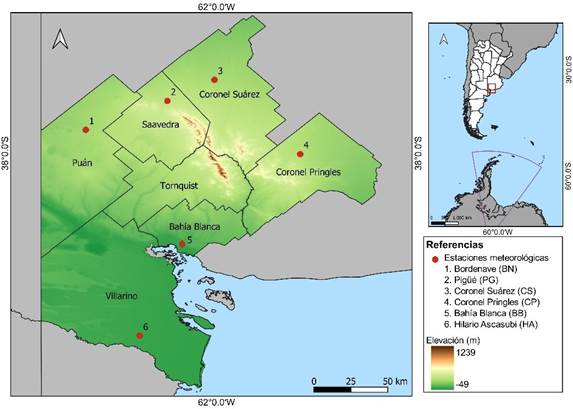
Figura 1. Área de estudio, ubicación en Argentina, elevación y ubicación las
estaciones meteorológicas.
Estaciones: Coronel Suárez,
(CS), Coronel Pringles
(CP), Pigüé (PG), Bordenave (BN), Bahía Blanca (BB) e Hilario Ascasubi
(HA). Fuente: elaboración propia.
Metodología
La etapa inicial del procedimiento implementado consiste en la obtención de la serie de precipitación mensual
del producto CHIRPS para el período 1990-2020, a través del sitio web
Climate Hazards Center (https://data.chc.ucsb.edu/products/CHIRPS-2.0/). Una vez recopilada la información
satelital, se compararon las estimaciones mensuales y anuales de CHIRPS con
datos de las 6 estaciones meteorológicas del Servicio Meteorológico Nacional (SMN) y del
Instituto Nacional de Tecnología Agropecuaria (INTA), presentes en el área,
para el periodo 1990 - 2020. Los datos del SMN se obtuvieron por pedido
específico por medio del contacto
institucional (https://www.argentina.gob.ar/smn/institucional/contacto) mientras
que, los datos
del INTA, se descargaron del Sistema de Información y Gestión
Agrometeorológica (https://siga.inta.gob.ar/#/). Las estaciones meteorológicas seleccionadas se describen en la Tabla 1, incluyendo Coronel Suárez, (CS), Coronel Pringles (CP), Pigüé (PG),
Bordenave (BN), Bahía Blanca (BB) e Hilario Ascasubi (HA).
La validación de bases de datos grillados requiere del
uso de fuentes independientes a las estaciones de anclaje utilizadas para su
estimación (Paredes- Trejo, Barbosa & Kumar,
2017). En el área de estudio estas
estaciones corresponden a las del SMN. No obstante, debido a la escasa
disponibilidad de información climática que caracteriza a la región, se emplearon los datos
de estas estaciones junto a los provistos por el INTA, considerada una fuente
externa. Precisamente la validación de esta base de datos se justifica en la
necesidad de recurrir a diversas fuentes de información que permitan suplir la
ausencia de registros hidroclimáticos continuos de
calidad.
|
IR
|
EM
|
|
Ubicación
|
Elevación (msnm)
|
|
SMN
|
Bahía Blanca
Aero
|
BB
|
38,43°S, 62,10
°W
|
83
|
|
INTA
|
Bordenave (EMC)
|
BN
|
37,85°S, 63,02°W
|
209
|
|
SMN
|
Coronel Pringles Aero
|
CP
|
38,00°S, 61,20°W
|
247
|
|
SMN
|
Coronel Suárez
Aero
|
CS
|
37,27°S, 61,53°W
|
233
|
|
SMN
|
Pigüé Aero
|
PG
|
37,36°S, 62,23°W
|
304
|
|
INTA
|
Hilario Ascasubi (EMC)
|
HA
|
39,38°S, 62,62°W
|
13
|
Tabla 1. Descripción de las estaciones meteorológicas utilizadas, institución
responsable (IR), nombre y sigla de la estación, ubicación y elevación (msnm).
Fuente: elaboración propia.
Para la comparación de las estimaciones de CHIRPS con los
datos de las estaciones meteorológicas, se llevó a cabo un análisis de punto a
píxel. Dicha metodología reduce la incertidumbre derivada
de la interpolación espacial de
estaciones meteorológicas que se encuentran distribuidas de forma desigual (Xu, Zou, Zhang &
Linderman, 2015; Cavalcante
et al., 2020). Finalmente, para
validar el rendimiento de CHIRPS
se aplicaron las siguientes métricas
estadísticas (Tabla 2): el
coeficiente de correlación de Pearson (r-Pearson), el error absoluto medio
(mae), el error cuadrático medio (rmse) y el porcentaje de sesgo (pbias), en entorno R utilizando
el paquete hydroGOF (Zambrano-Bigiarini,
2022).
|
Métrica estadística
|
Ecuación
|
VO
|
|
r-Pearson
|
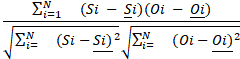
|
1,0
|
|
mae
|
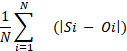
|
0,0
|
|
rmse
|
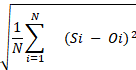
|
0,0
|
|
pbias
|
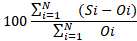
|
0,0
|
Tabla 2. Descripción de métricas estadísticas utilizadas para evaluar el
rendimiento de CHIRPS. Coeficiente de correlación de Pearson (r-Pearson), error absoluto medio
(mae), error cuadrático medio (rmse), porcentaje de sesgo (pbias). N es
el número total de observaciones, S representa los datos CHIRPS y O los datos observados, en un período i. VO: valor óptimo. Fuente: elaboración
propia.
El coeficiente de correlación de Pearson cuantifica la
relación lineal entre las estimaciones y
las observaciones in situ, oscilando entre -1,0 y 1,0
(Paredes-Trejo et al., 2017). Por otra parte, el error absoluto
medio (mae) refleja la magnitud promedio de las estimaciones del error, adquiriendo sólo valores positivos
(Paredes-Trejo et al.,
2017). El error cuadrático medio (rmse) determina el
grado promedio de error en las
estimaciones respecto a las observaciones y adquiere sólo valores positivos,
que en este caso se representa en milímetros
(Anjum et
al., 2022). Por último, el porcentaje de sesgo mide la tendencia promedio
de los valores estimados, tomando valores porcentuales positivos o negativos
(Paredes-Trejo et al., 2017).
Resultados y Discusión
Distribución de la precipitación mensual.
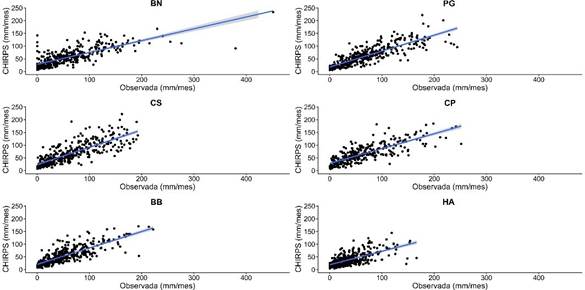
La Figura 2 representa la dispersión entre la precipitación
observada en las estaciones meteorológicas y la precipitación estimada por CHIRPS a
escala mensual (1990-2020). La línea azul indica regresión lineal y el área sombreada indica
el nivel
de
confianza del 95%. En el caso de BB, PG y BN, CHIRPS muestra una
sobreestimación en valores bajos (hasta 50 mm/mes) y una subestimación de la
precipitación en valores
superiores. En HA sobreestima hasta los 25 mm, en CP hasta 70
mm/mes y en CS sobreestima hasta los 75 mm/mes. Por encima de dichos valores, en todos los casos, tiende a
subestimar. En otras palabras, el producto CHIRPS muestra una sobreestimación
en valores bajos y una subestimación en valores altos, siendo diferente el
punto de quiebre según la estación. Este comportamiento es consistente con lo
hallado por Cavalcante et al. (2020) y Paredes-Trejo et
al. (2017) en Brasil y por Medina et
al. (2023) en el norte argentino.
Figura 2. Diagramas de dispersión de la precipitación observada en las estaciones
meteorológicas frente a la estimada por CHIRPS a escala mensual (1990-2020). La
línea azul indica regresión lineal
y el área sombreada indica el nivel de confianza
del 95%. Fuente: elaboración propia sobre la base de datos del SMN y
datos CHIRPS.
Validación mensual del producto
CHIRPS.
La tabla 3 muestra las medidas de desempeño de CHIRPS a escala mensual.
Los valores del coeficiente de correlación de Pearson (r-Pearson)
indican un buen ajuste entre los datos observados y las estimaciones en la
mayoría de las estaciones, con valores superiores a 0,70 en la mayoría de las
estaciones, siendo Hilario Ascasubi la excepción con 0,68, y destacándose Pigüé con 0,84. Los valores
más bajos, registrados en Hilario Ascasubi coinciden
con lo observado en el noroeste argentino y puede deberse a una característica observada en CHIRPS para condiciones climáticas secas,
debido a que posee menor capacidad para detectar lluvias más ligeras (Medina et al. 2023). Con respecto al error absoluto medio (mae), se reconocen mayores errores
en el centro y norte del área de estudio, particularmente en BN y CP donde los valores
oscilan
entre 24,4 y 22,3 mm respectivamente. Por el contrario, los valores más
cercanos al óptimo se encuentran en HA y BB con errores de 17,8 y 18,3 mm respectivamente.
Por otra parte, el error cuadrático
medio (rmse), asociado con el grado de error en la estimación, varía entre 23,9 y 37,8 mm, siendo
mejor el rendimiento de CHIRPS en HA y BB
donde el rmse fue de 23,9 y 24,9 mm respectivamente.
Es decir, tanto con mae como con rmse, los mayores
errores se hallaron en las estaciones próximas al cordón serrano. Por tal motivo es necesario
profundizar el análisis
en el área serrana con el fin de corroborar la aplicabilidad de la base de datos. Por último, el porcentaje de sesgo (pbias)
presenta diferencias, sin un patrón claro entre las estaciones analizadas. Las estaciones que presentan valores negativos son BN y
PG con -4,7 y -
11,1%, por lo tanto, en estos casos tiende ligeramente a subestimar. En las
restantes estaciones tiende a sobreestimar, en valores que no superan el 5%.
Los valores más cercanos al óptimo se localizaron en HA y CP, con 2,4 y 3,5%.
Estos valores se comparan con los hallados por Cerón, Molina-Carpio, Ayes
Rivera, Andreoli, Kayano y Canchala (2020), quienes para el sur de la Cuenca del Plata
obtuvieron sesgos que van entre 0 y 15% de subestimación en el primer caso y de
entre 0 y 15% de sobreestimación en las dos restantes, coincidiendo con las estaciones de PG, CS y BB. Por lo tanto, es posible afirmar que
CHIRPS representa adecuadamente los sistemas de precipitación dominantes, a
diferencia de lo que ocurre en Mendoza donde la sobreestimación puede superar los
100 mm/mes (Rivera et al., 2018). Sin
embargo, cabe destacar que la correlación en el área de estudio
adquiere mayores valores
en las estaciones de anclaje
de CHIRPS respecto a las fuentes independientes.
|
Métrica
estadística
|
CS
|
CP
|
PG
|
BN
|
BB
|
HA
|
|
r-Pearson
|
0,80
|
0,80
|
0,84
|
0,77
|
0,81
|
0,68
|
|
mae
|
21,36
|
22,33
|
20,21
|
24,38
|
18,33
|
17,77
|
|
rmse
|
29,23
|
30,33
|
29,75
|
37,80
|
24,94
|
23,89
|
|
pbias
|
4,40
|
3,50
|
-11,10
|
-4,70
|
3,70
|
2,40
|
Tabla 3. Desempeño de CHIRPS
a escala mensual en estaciones del suroeste de la provincia de Buenos Aires
(1990-2020). Coeficiente de correlación de Pearson (r- Pearson), error absoluto
medio (mae), error cuadrático medio (rmse),
porcentaje de sesgo (pbias). Estaciones: Coronel Suárez, (CS), Coronel Pringles (CP), Pigüé (PG), Bordenave (BN), Bahía
Blanc (BB) e Hilario Ascasubi (HA). Fuente: elaboración propia.
Distribución de la precipitación anual.
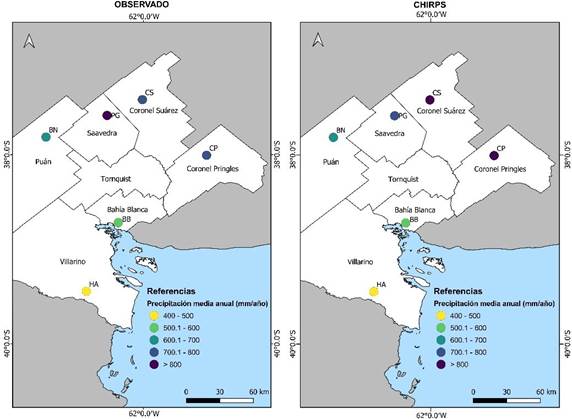
De forma comparativa se analizó también la distribución
espacial de la precipitación media anual para el período 1990-2020 entre lo
observado en las estaciones meteorológicas y lo estimado
por CHIRPS (Figura
3). En el área de estudio,
las precipitaciones varían entre 752,3 mm al este (CP) y 704,4 mm al oeste (BN),
mientras
que de norte a sur oscilan entre 778,8 (CS) y 454,3 mm (HA). Es decir que
decrecen en sentido noreste-suroeste. Esto coincide con lo hallado por Casado y
Campo (2019) para el período 1977-2010. La variabilidad en los montos de
precipitación se encuentra determinada por los efectos de la continentalidad,
la topografía regional y la conjugación de fenómenos atmosféricos de pequeña a
gran escala (Campo, Ramos & Zapperi, 2009; Casado & Campo, 2019).
Las estaciones que presentan mayor variación en la estimación
de la precipitación media anual (1990- 2020) se ubican en el noreste del área de estudio:
CS sobreestima 34.3 mm y CP 26,1 mm mientras que en PG subestima 91,1 mm. Estos valores
representan 4,4%, 3,5% y 11,1% de la precipitación media
anual, respectivamente.
Figura 3. Distribución espacial de la precipitación media anual para el período
1990- 2020 entre datos observados y estimación de CHIRPS. Estaciones: Coronel Suárez, (CS), Coronel Pringles (CP), Pigüé (PG),
Bordenave (BN), Bahía Blanc (BB) e Hilario Ascasubi (HA). Fuente: elaboración propia sobre la base de datos del SMN y
datos CHIRPS.
A escala anual (Figura 4), la comparación entre la
precipitación observada y la estimada por CHIRPS muestra el mismo patrón que en
el caso de la escala mensual. Es decir, tiende
a sobreestimar en valores reducidos y a subestimar la precipitación en valores altos. En la estación de HA,
CHIRPS sobreestima hasta los 500 mm/año y a partir de allí subestima. En BN, la tendencia a la
sobreestimación encuentra su límite
alrededor de los 625 mm/año,
en Pigüé a los 650 mm/año, en BB a
los 700 mm/año. Por último, en PG sobreestima hasta los 800 mm/año y en CS hasta los 850 mm/año, para luego subestimar los montos
de precipitación.
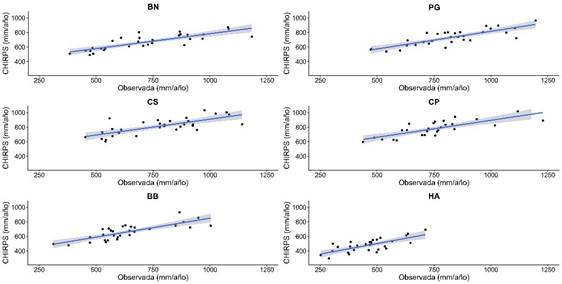
Figura 4. Diagramas de dispersión de la precipitación observada en las
estaciones meteorológicas frente a la estimada
por CHIRPS a escala anual (1990-2020). La línea
azul indica regresión lineal y el área sombreada indica
el nivel de confianza del 95%.
Estaciones: Coronel Suárez, (CS), Coronel Pringles
(CP), Pigüé (PG), Bordenave (BN), Bahía Blanc (BB) e Hilario Ascasubi (HA).
Fuente: elaboración propia sobre la base de datos del SMN y datos CHIRPS.
Validación anual del producto
CHIRPS.
Paralelamente, se analizó el desempeño de la base de
datos CHIRPS a escala anual (Tabla 4).
El coeficiente de correlación de Pearson demostró
un buen ajuste en todos los casos, registrando valores superiores a 0,70
y de hasta 0,82 en el caso de Pigüé. Se
observan menores diferencias en los resultados de las correlaciones entre
estaciones de anclaje de la base de datos y las fuentes independientes,
respecto a los desempeños a escala mensual. En cuanto a las estadísticas de
error, el error absoluto medio fue mayor en las estaciones ubicadas al norte:
Bordenave 132,0 mm, Pigüé 113,1 mm y CS 106,6
mm. Por otra parte, el error medio cuadrático fue
mayor al oeste (Bordenave 182,3 mm) y menor hacia el sur (Hilario Ascasubi 79,5
mm). El patrón espacial de decrecimiento de la precipitación en sentido
noreste-suroeste es reproducido de manera correcta por CHIRPS. No obstante, en las estaciones ubicadas al oeste del sistema de Ventania (PG y BN), las
estimaciones de CHIRPS mostraron una subestimación, mientras que en las
ubicadas al este (CS y CP) presentaron sobreestimaciones. Estas diferencias
pueden estar relacionadas con la presencia del sistema de Ventania. La influencia de sistemas montañosos sobre las estimaciones de CHIRPS ha sido descripto también
por Rivera et al. (2018) para el caso de los Andes Centrales. Estos mismos autores
hallaron sesgos vinculados a la estación
lluviosa que se trasladan
a las precipitaciones anuales y que en algunos casos, como en el norte
de
la
provincia de Neuquén, superan el 50% de sobreestimación. En el caso del área de
estudio, a escala anual el porcentaje de sesgo presentó igual patrón que a
escala mensual: en PG y BN subestima -11,1 % y -4,7%, respectivamente, mientras
que en el resto de las estaciones sobreestima entre 3,5 y 4,4%.
|
Métrica estadística
|
CS
|
CP
|
PG
|
BN
|
BB
|
HA
|
|
r-Pearson
|
0,74
|
0,78
|
0,82
|
0,71
|
0,79
|
0,72
|
|
mae
|
106,58
|
89,78
|
113,14
|
132,04
|
79,63
|
63,69
|
|
rmse
|
134,76
|
117,64
|
144,56
|
182,29
|
101,72
|
79,51
|
|
pbias
|
4,40
|
3,50
|
-11,10
|
-4,70
|
3,70
|
4.00
|
Tabla 4. Desempeño de CHIRPS
a escala mensual en estaciones del suroeste de la provincia de Buenos Aires
(1990-2020). Coeficiente de correlación de Pearson (r- Pearson), error absoluto
medio (mae), error cuadrático medio (rmse),
porcentaje de sesgo (pbias). Estaciones: Coronel Suárez, (CS), Coronel Pringles (CP), Pigüé (PG), Bordenave (BN), Bahía
Blanc (BB) e Hilario Ascasubi (HA). Fuente: elaboración propia.
Conclusiones
En el presente
trabajo se presenta
la validación del producto CHIRPS
respecto a su capacidad de
estimar precipitación en el suroeste de la provincia de Buenos Aires para el período
1990-2020. El rendimiento de CHIRPS se evaluó a partir del contraste
con datos observados de estaciones meteorológicas del SMN y del INTA. Se concluye
que la variabilidad anual y mensual de la precipitación se encuentra bien representada,
con un ajuste que oscila entre 0,68 y 0,84, según la estación meteorológica.
Sin embargo, se detectaron ligeros sesgos
de subestimación en los casos de
Bordenave y Pigüé, entre -4,7 y
-11,1% mientras que en las estaciones
restantes CHIRPS tendió a sobreestimar en hasta 4,4%. Asimismo, se observaron
diferencias en el ajuste en las estaciones de anclaje de la base de datos y las
independientes, siendo superior la correlación en las primeras. Estas
diferencias fueron más pronunciadas en la escala mensual. De esta manera el uso
de la base de datos es más apropiada para estudios climáticos a escala anual.
Teniendo presentes estas consideraciones, CHIRPS
es aplicable al análisis de las
precipitaciones en el suroeste de la provincia de Buenos Aires, a pesar de que
se requiere una profundización en la validación en el área serrana. Asimismo,
se plantea la necesidad de
validación de esta base de datos a escala diaria, para ampliar sus posibles aplicaciones en el área de estudio,
particularmente para el estudio de eventos
extremos. Si bien el uso de estimaciones de precipitación presenta
limitaciones, resulta un recurso de interés para aplicar en regiones donde los
registros observacionales son escasos o no poseen una adecuada cobertura espacio-temporal.
Agradecimientos
El
presente trabajo se desarrolló en el marco del PGI Geografía Física aplicada al
estudio de la interacción sociedad-naturaleza. Problemáticas ambientales a diferentes escalas témporo-espaciales
(24/G092), financiado por la Secretaría General de Ciencia y Tecnología (SGCyT), Universidad Nacional del Sur. Yamila Lambrecht y Anabella Montico son
estudiantes del Doctorado en Ciencias Aplicadas Mención Ambiente y Salud
(DCAAS, UNICEN, Argentina).
Referencias
Aliaga, V. S., Ferrelli, F.
& Piccolo, M. C. (2017). Regionalization of climate over the Argentine Pampas. International
journal of climatology, 37, 1237-1247. https://doi.org/10.1002/joc.5079
Alsilibe,
F., Bene, K., Bilal, G., Alghafli, K. & Shi, X. (2023). Accuracy
Assessment and Validation of Multi-Source CHIRPS Precipitation Estimates
for Water Resource Management in the Barada Basin,
Syria. Remote Sensing, 15 (7), 1778. https://doi.org/10.1002/qj.3244
Anjum, M. N., Irfan,
M., Waseem, M., Leta, M. K., Niazi, U. M., ur Rahman, S., Ghanim, A., Ahsan Mukhtar, M., & Nadeem,
M. U. (2022). Assessment of PERSIANN-CCS, PERSIANN-CDR, SM2RAIN-ASCAT, and CHIRPS-2.0 rainfall products over a semi-arid
subtropical climatic region. Water, 14(2), 147. https://doi.org/10.3390/w14020147
Arregocés, H. A., Rojano,
R. & Pérez,
J. (2023). Validation of the CHIRPS dataset
in a coastal region with extensive plains and complex topography. Case
Studies in Chemical and Environmental
Engineering, 8. https://doi.org/10.1016/j.cscee.2023.100452
Ávila-Parra, K. & Martín-Vide, J. (2013). Análisis
estadístico de los eventos extremos de precipitación. Cuadernos
Geográficos de la Universidad de Granada, 52(1),
69-
83. https://dialnet.unirioja.es/servlet/articulo?codigo=4298593
Bai,
L., Shi, C., Li, L., Yang, Y. & Wu, J. (2018). Accuracy of CHIRPS
Satellite- Rainfall Products
over Mainland China. RemoteSensing, 10(3),
362.
https://doi.org/10.3390/rs10030362
Bezerra, B. G., Silva, L. L., Santos e
Silva, C. M. & de Carvalho, G. G. (2019). Changes of precipitation extremes indices in São Francisco River Basin, Brazil
from 1947 to 2012. Theoretical
and Applied Climatology, 135, 565-576.
https://doi.org/10.1007/s00704-018-2396-6
Campo, A., Diez, P. & Capelli de Steffens, A. (2004). El clima del suroeste bonaerense, Bahía
Blanca, República Argentina, EdiUNS.
Campo, A.; Ramos, B. & Zapperi,
P. (2009). Análisis de las variaciones
anuales de precipitación en el suroeste bonaerense, Argentina. 1–12. http://observatoriogeograficoamericalatina.org.mx/egal12/Procesosambientales/Cl imatologia/16.pdf
Casado, A. &
Picone, N. (2018). Aplicabilidad de los datos grillados para el análisis
espaciotemporal de las precipitaciones, provincia de Buenos Aires (Argentina). Párrafos Geográficos, 17(1), 46-62.
http://igeopat.org/parrafosgeograficos/images/RevistasPG/2018_17_1/29-3.pdf Casado,
A. L. & Campo, A. M. (2019).
Extremos hidroclimáticos y recursos hídricos:
estado de conocimiento en el suroeste bonaerense, Argentina. Cuadernos Geográficos, 58(1), 6-26. http://dx.doi.org/10.30827/cuadgeo.v58i1.6751
Cavalcante, R. B. L., da Silva Ferreira, D. B., Pontes, P. R. M., Tedeschi, R.
G., da Costa, C. P. W. &
de Souza, E. B. (2020).
Evaluation Cavalcante of extreme rainfall indices from CHIRPS
precipitation estimates over the Brazilian Amazonia. Atmospheric Research, 238, 104879. https://doi.org/10.1016/j.atmosres.2020.104879
Cerón, W. L., Molina-Carpio, J., Ayes Rivera,
I., Andreoli,
R. V., Kayano,
M. T., & Canchala, T. (2020). A principal component analysis
approach to assess CHIRPS precipitation dataset for the study of climate
variability of the La Plata Basin, Southern South America.
Natural Hazards, 1 03(1), 767-783.https://doi.org/10.1007/s11069-020-04011-x
de MoraesCordeiro, A. L. & Blanco,
C. J. C. (2021). Assessment of satellite products for filling rainfall data gaps in the Amazon region. Natural Resource
Modeling, 34(2), e12298. https://doi.org/10.1111/nrm.12298
Fourier, F. (1960). Climat et erosion; la relation entre l’erosion du sol par l’eau et les
precipitations atmospheriques. Paris, Francia, Presses universitaires de France.
Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., Husak, G.,
Rowland, J., Harrison, L., Hoell, A. & Michaelsen, J. (2015). The climate hazards infrared
precipitation with stations—a new environmental record for monitoring extremes.
Scientific data, 2(1), 1-21. https://doi.org/10.1038/sdata.2015.66
Gentili, J. O. & Gil, V. (2013). Variabilidad temporal de las precipitaciones en vertientes opuestas del
Sistema de Ventania, Buenos Aires, Argentina. Revista Universitaria de Geografía, 22(2),
147-166.
https://www.redalyc.org/pdf/3832/383239184008.pdf
Gil, V., Gentili,
J., Campo, A. M., Jelinski, G. & Crisafulli, M. (2016). Evaluación del peligro potencial de crecidas en cuencas serranas. Sistema
de Ventania, provincia de Buenos Aires. III
Encuentro de Investigadores en Formación en Recursos Hídricos, Ezeiza, Argentina. https://www.ina.gov.ar/ifrh- 2016/trabajos/IFRH_2016_paper_133.pdf
Gusmerotti,
L. A., Posse, G., Oricchio,
P. A., Rivadeneira, S. T. & Di Bella, C. M. (2023). Evaluation of Satellite-Based
Precipitation Estimates and a Correction Methodology Through Weather Stations
in Córdoba (Argentina). https://dx.doi.org/10.2139/ssrn.4374156
Hobouchian, M. P., Salio,
P., Skabar, Y. G., Vila, D. & Garreaud,
R. (2017). Assessment
of satellite precipitation estimates over the slopes of the subtropical Andes. Atmospheric
Research, 190, 43-54. https://doi.org/10.1016/j.atmosres.2017.02.006
Lovino, M. A. (2015). Impacto ambiental de la variabilidad climática y los
eventos extremos en la provincia de Santa Fe, en el contexto del cambio climático
(Tesis

doctoral). Universidad Nacional del Litoral, Santa Fé,
Argentina. http://hdl.handle.net/11185/707
Lúgaro,
T. (2022). Caracterización climática de los vientos en Argentina a partir de datos
observados y satelitales (Tesis de grado). Universidad de Buenos Aires,
Buenos Aires, Argentina. https://anemoi.net.ar/static/img/Tesis_Lugaro.pdf
Marianetti,
G. & Rivera, J. (2021). Riesgos asociados a eventos de precipitaciones
intensas en la región oeste del Gran Mendoza, Argentina. ICU: Investigación, Ciencia y Universidad,
5(6), 31-42.https://doi.org/10.59872/icu.v5i6.369
Martín‐Vide,
J. (2004). Spatial distribution of a daily precipitation concentration index in
peninsular Spain. International Journal
of Climatology, 24(8), 959-971. https://doi.org/10.1002/joc.1030
Medina, F. D., Zossi,
B. S., Bossolasco, A. & Elias, A. G. (2023).
Performance of CHIRPS dataset for monthly and annual rainfall-indices in
Northern Argentina. Atmospheric Research, 283,
106545.https://doi.org/10.1016/j.atmosres.2022.106545
Mianabadi, A. (2023). Evaluation of long-term
satellite-based precipitation products for developing intensity-frequency (IF)
curves of daily precipitation. Atmospheric
Research, 286, 106667. https://doi.org/10.1016/j.atmosres.2023.106667
Olmo, M.
E. (2023). Cambios futuros de la
precipitación extrema en el sudeste de Sudamérica: modelado climático
estadístico regional y patrones de circulación sinóptica (Tesis Doctoral). Universidad de Buenos Aires,
Buenos Aires, Argentina. http://hdl.handle.net/20.500.12110/tesis_n7282_Olmo
Ombadi,
M., Nguyen, P., Sorooshian,
S. & Hsu, K.
L. (2018). Developing
intensity‐ duration‐frequency (IDF) curves from satellite‐based precipitation:
Methodology and evaluation. Water Resources Research, 54(10), 7752-7766.
https://doi.org/10.1029/2018WR022929
Paredes-Trejo, F. J.,
Barbosa, H. A. & Kumar, T. L. (2017). Validating CHIRPS- based satellite
precipitation estimates in Northeast Brazil. Journal of arid environments, 139,
26-40. https://doi.org/10.1016/j.jaridenv.2016.12.009
Prakash, S. (2019).
Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation
products across India. Journal of
hydrology, 571, 50-59. https://doi.org/10.1016/j.jhydrol.2019.01.036
Rivera, J. A., Marianetti, G. & Hinrichs, S. (2018). Validation of
CHIRPS precipitation dataset along
the Central Andes of Argentina. Atmospheric Research,
213, 437-449. https://doi.org/10.1016/j.atmosres.2018.06.023
Robledo, F. A., Penalba, O. C., & Bettolli,
M. L. (2013). Teleconnections between tropical‐extratropical oceans and the
daily intensity of extreme rainfall over Argentina. International Journal of Climatology, 33(3), 735-745.
https://doi.org/10.1002/joc.3467
Salih, W., Epule, T. E., EL Khalki, E. L., Ouatiki, H., Erraki, S., Achli, S. & Chehbouni, A.
(2023). A comprehensive assessment of satellite precipitation products over a semi-arid region: focus on extreme events. Natural Hazards,
1-29. https://doi.org/10.1007/s11069-023-06317-y
Saucedo, G. I., Kurtz, D. B. & Contreras, F. I. (2023).
Validación de precipitaciones estimadas mediante satélites
para dos estaciones de la provincia
de Corrientes
(República
Argentina). Contribuciones Científicas,
35(1), 46-53. https://gaea.org.ar/contribuciones/CC_GAEA_35.pdf#page=47
Serrano‐Notivoli, R., Beguería, S., Saz, M. Á. and De Luis, M. (2018).
Recent trends reveal decreasing intensity of daily
precipitation in Spain. International Journal of Climatology, 38(11), 4211-4224.
Volonté,
A. (2017). Geomorfología fluvial aplicada
al peligro de crecidas: cuenca del arroyo San Bernardo, sistema de Ventania,
Argentina (Tesis Doctoral), Universidad Nacional del Sur, Departamento de
Geografía y Turismo, Bahía Blanca, Argentina. http://repositoriodigital.uns.edu.ar/handle/123456789/3453
Wischmeier, W. H. (1959).
A rainfall erosion
index for a universal soil‐loss equation. Soil Science
Society of America Journal, 23(3), 246-249. https://doi.org/10.2136/sssaj1959.03615995002300030027x
Xu,
W., Zou, Y., Zhang, G. & Linderman, M. (2015). A comparison among spatial
interpolation techniques for daily rainfall data in Sichuan Province, China. International Journal of Climatology, 35(10),2898-2907.
https://doi.org/10.1002/joc.4180
Zambrano, F., Wardlow,
B., Tadesse, T., Lillo-Saavedra, M. & Lagos, O. (2017). Evaluating
satellite-derived long-term historical precipitation datasets for drought
monitoring in Chile. Atmospheric Research, 186, 26-42.
https://doi.org/10.1016/j.atmosres.2016.11.006
Zambrano-Bigiarini, M. (2022).Packageh.
ydroGOF. https://cran.r-project.org/web/packages/hydroGOF/index.html
 Boletín geográfico. Año XLVI. N°46 - 2024, pp. 1-16 Departamento Geografía. Universidad Nacional
Boletín geográfico. Año XLVI. N°46 - 2024, pp. 1-16 Departamento Geografía. Universidad Nacional![]()